圆角
1.border-radius 圆角边框
2.box-shadow 阴影框
3.border-image （不支持ie）边界图片

背景
1.background-image
2.background-size
3.background-origin 指定背景图片的位置区域（border-box, padding-box, content-box）
4.background-clip 背景剪裁（指从指定位置开始绘制）

渐变（gradients）
1.linear-gradient 线性 background: linear-gradient(direction,color-stop1,color-stop2,..)
其中参数direction包括预定义的：to bottom、to top、 to right等，也可以使用角度angle；
0deg 从下到上、90deg 从左到右；
2.radial-gradient 径向 background: radial-gradient(center,shape,size,start-color,…,last-color)
shape参数：circle、ellipse等；
size参数定义渐变大小：closest-side、farthest-side、closest-corner、farthest-corner(默认)
3.repeating-linear-gradient(red,yellow 10%,green 20%) 重复线性渐变

透明度（transparency）
rgba()最后一个参数0～1

文本效果
1.text-shadow
2.box-shadow
3.text-overflow 属性值包括：clip(修建文本)、ellipsis(显示省略号)
4.word-wrap
5.word-break 自动换行：break-all(允许在单词内换行)、keep-all(只能在半角空格或连字符处换行)

2D转换
1.translate() x,y平移
2.rotate() xdeg顺时针旋转
3.scale() x,y 增大／减小
4.skew() xdeg,ydeg 倾斜坐标系
5.matrix() 表示矩阵，需要六个参数

matrix() 方法把所有 2D 转换方法组合在一起。
matrix() 方法需要六个参数，包含数学函数，允许：旋转、缩放、移动以及倾斜元素。
matrix()中的6个参数代表了一个3*3的矩阵（线性代数）。

平移
在CSS3中我们矩阵的原始值是这样的
transforms:matrix(1,0,0,1,0,0);
写成我们数学里矩阵的形式是这样的

这么看起来，我们不太好分辨哪个数字对应的是我们上面写的matrix值里的哪一个，那为了便于描述我们把它写成：
transforms:matrix(a,b,c,d,e,f);
那么写成数学矩阵式就是这样的：

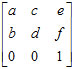
根据我们上面说的用矩阵与向量的乘法来施加运动，我们就可以来看一下它到底是怎么运动起来的

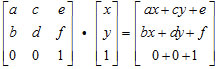
这么一来我们可以得到一个式子就是：
x’=ax+cy+e
y’=bx+dy+f

x’和y’就是我们变换后的水平位置坐标和垂直位置坐标，现在我们想要把元素往x轴的正方向平移10，在y轴方向上不动,反映到方程式里，我们要怎么来实现呢

元素往x轴的正方形平移10，在y轴方向上不动，反映到方程式里：

x’=ax+cy+e —（x’=ax+cy+e+10)

y’=bx+dy+f （不变）

元素往y轴的正方向平移10，在x轴方向上不动，反映到方程式里：

x’=ax+cy+e （不变）

y’=bx+dy+f —（y’=bx+dy+f+10）

元素同时往x轴正向和y轴正向移动10个单位 ：

我们用css矩阵来写：transform： matrix（1,0,0,1,10,10）–其他数值都不动，e和f分别加10

结论：平移只有跟e和f有关系，跟其他a,b,c,d没有关系，它们该怎么样还是怎么样，e对应x轴的平移，f对应y轴的平移，往正方向平移多少单位就加上多少单位，反之则减去多少个单位。

缩放
平移就是x或者y加减一个常数来得到的，理解了平移之后缩放就很简单了，可不就是x和y的倍数发生了变化么，反映到式子上来那就是系数的变化，那同样道理我们把上面的式子拿过来

x放大2倍 y不变

x’=ax+cy+e—（x’=2ax+cy+e) 就是x的系数增大2倍

y’=bx+dy+f (不变)

y放大2倍 x不变

x’=ax+cy+e (不变)

y’=bx+dy+f—(y’=bx+2dy+f)

就是y的系数增大2倍x和y都放大2倍，就是x和y的系数都增大2倍写成矩阵就是：

transform：matrix（2,0,0,2,0,0)

结论：缩放只有跟a和b有关系，跟其他数值都无关，a对应x轴缩放，b对应y轴缩放，缩放多少倍就乘以多少

旋转
相比于平移和缩放，旋转相对来说要复杂点了，当然搞清楚了就没什么难的了

transform：matrix（cosθ，-sinθ,sinθ,cosθ,0,0);

现在我们要让这个元素往顺时针方向旋转45°（sin45°=0.707，cos45°=0.707），那么我们给div加样式如下：

transform: matrix(0.707,0.707,-0.707,0.707,0,0);

这个div是不是就按我们预期的一样往顺时针方向转了45°了；

接下来我们把这个旋转放到数学里来看下
那同样的我们把它写成数学里矩阵的形式：

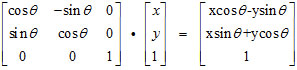
同样的根据矩阵的计算公式，我们可以得到公式：

x’=xcosθ-ysinθ; y’=xsinθ+ycosθ

现在我们先把公式放在这里，我们来看一下下图的这个正方形，从图中我们可以知道a,b,c,d的坐标分别为：

A(0,1) B(1,1) C(1,0) D(0,0)

当我们让它旋转90°之后，那此时的cos45°就是0 sin45°都为1，分别把A,B,C,D里的x,y代入上面的公式之后我们可以得到：

现在这个正方形就变成了下图的样子，和我们写代码达到的效果是一样的：

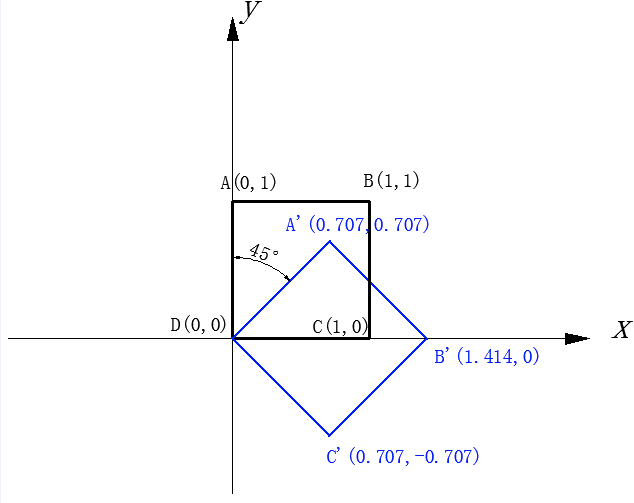
结论：我们要记住初始写法是这样的
transform：matrix（cosθ，-sinθ,sinθ,cosθ,0,0);然后需要旋转多少度就计算出这个度数的cosθ，sinθ就可以达到我们想要的效果

3D转换
1.translate3d(x,y,z)
2.scale3d(x,y,z)
3.rotate3d(x,y,z,angle)

过渡
transition:width 2s,height 2s,transform 2s;

动画 @Keyframes规则、animation属性

@Keyframes mymove
{ 
    from {top:0px;}
    to {top:200px;}
}

div

{ 
    animation:mymove 5s infinite;
    -webkit-animation:mymove 5s infinite; /* Safari 和 Chrome */
}

多列
1.column-count 指定元素的列数
2.column-gap xpx 指定列之间的距离
3.column-rule 设置列之间的宽度、样式、颜色
4.column-rule-color
5.column-rule-style
6.column-rule-width
7.column-width